Harmonic errors in single-chain-of-equal-fifths tunings
by David C Keenan, 4-Nov-1998
last updated 19-Jul-2000

http://users.bigpond.net.au/d.keenan

Alien landscapes? Click on a chart to see the full sized version.

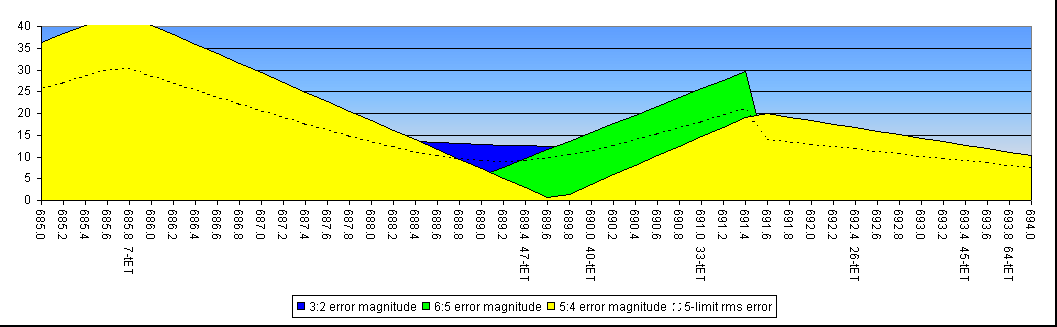
Errors in 5-limit intervals (explained below)

Errors in 7-limit intervals (explained below)

In this document, "single-chain-of-equal-fifths tunings" refers to those octave-based tunings whose notes within each octave may be considered to be generated by a single chain of uniform fifths, whether the chain be closed (called a "cycle of n fifths" or "n-tone equal temperament") or open (e.g. the various meantones). A "fifth" here is any usable approximation to a 2:3 frequency ratio. An n-tone equal temperament (n-tET) is a tuning where the octave is divided into n equal divisions. The tuning commonly called simply "equal temperament" is thus 12-tET. A "tuning" is here distinguished from a "scale", where a scale is the set of notes (per octave) actually chosen for use in some situation, whereas, in the case of an open tuning, the number of notes in the tuning is potentially infinite. So a scale is here a subset of a tuning. This is similar to the relationship between a mode and a scale.

We assume here that it is desirable for tunings to provide good approximations to small-whole-number frequency ratios for purposes of harmony. All notes are assumed to be repeated at perfectly tuned octaves (1:2) and therefore factors of two may be ignored or included without changing any of the following results.

Single-chain-of-equal-fifths is a very large and significant class of tunings, but note that not all equal-tempered scales are members of this class, since some consist of 2 or more closed chains of fifths, equally spaced within the octave. Well temperaments are not in this class because they have more than one size of usable fifth. Just tunings are not in this class because their intervals (other than fifths) are not generated or approximated by chains of fifths at all. Non-octave tunings are also not included here.

Each set of four charts above, shows on a horizontal axis, a spectrum of generalised fifths (approximations to 2:3) ranging in size from 685 to 721 cents, in increments of 0.2 cents. The spectrum is split into four sections for convenience of display. I have also shown the approximate position of all the relevant equal tempered tunings (ETs) up to 72. If an ET doesn't appear here, it's because its fifths are either:
much too narrow (2, 4, 9, 11, 16, 23) or
much too wide (1, 3, 6, 8, 13, 18) or
it has more than one chain of fifths:
2 chains: 4, 6, 10, 14, 24, 34, 38, 44, 52, 54, 58, 62
3 chains: 15, 21, 36, 51, 57, 66
4 chains: 20, 28, 48, 68
5 chains: 25, 35, 60
6 chains: 30, 72.

Incidentally, the fifth size for a multi-chain ET is the same as that for the ET obtained by dividing by the number of chains. e.g. 72-ET has the same fifth size as 72/6 = 12-ET. Those with multiple chains may have more going for them than their fifth size, but I do not address this here. Similar charts could be produced for each class of multi-chain open tunings, which would include these ETs. Two-chain tunings are addressed in a sequel entitled Harmonic errors in double-chain-of-equal-fifths tunings.

I have also shown on the horizontal axis the approximate position of some historical meantone tunings and Pythagorean tuning. In fact these charts were inspired by Margo Schulter's meantone spectrum chart.
http://www.medieval.org/emfaq/harmony/pyth5.html#6.2

Note that fifths outside the approximate range of 692 to 712 cents (max 10 cent error) are often considered unusable wolves based on various people's perception of their consonance, but there is no sharp cutoff. I wish to propose a different definition of wolves that comes from the mathematics of chains of fifths. From 714.9 cents up to 720 cents (5-tET), a chain of 6 fifths produces a better 2:3 than the fifths making up the chain. Similarly from 689.3 cents down to 685.7 cents (7-tET), a chain of 8 fifths produces a better 2:3 than the fifths making up the chain. This provides a handy functional definition of a wolf fifth for our purposes, namely any fifth for which some chain of less than 11 (±) gives a better approximation of 2:3. This corresponds to any fifth outside the range 689.3 to 714.9 cents, i.e. any fifth with an error outside -12.7 to +12.9 cents.

Some authors use the term meantone to refer to all of the tunings considered in this paper. I object to this on historical grounds and use it to refer only to the region between 691.5 cents and 700.0 cents. Although this is still broader than the historical usage it is the region where 4 fifths remains the best approximation to a major third (4:5), within a 12 note scale.

On a similar basis I also refer below to the Pythagorean region as between 700.0 and 705.8 cents and the super-Pythagorean region (around 22-tET) as between 705.8 and 711.8 cents.

The vertical axis represents the magnitude (absolute value) of the harmonic errors in cents. That is, it does not show whether the error is positive or negative (wide or narrow) only its size. The harmonic error in an interval is here defined as the difference in cents between its width in just intonation (a small-whole-number ratio of frequencies) and the nearest approximation obtained by stacking the given size of fifths or fourths (fifths in reverse) and eliminating octaves.

If there was no limit to the number of fifths or fourths we could stack to approximate a given ratio we could approximate any ratio as closely as we liked with any size of fifth, but there are practical limits. I somewhat arbitrarily chose a limit of ±14 fifths for the approximations to 4:5 and 4:7. Note that this is not a limit on the number of notes in a scale, but if a scale contains more than 15 consecutive notes in a chain of fifths, or spans more than 14 such fifths whether or not all their endpoints appear in the scale, then it might contain a better approximation to some ratio than that shown on the charts. However it will be very difficult to make use of an approximation that appears in only one or two positions and is so many fifths distant.

For example, -14 fifths (14 fourths) allows an approximation to 4:7 in the Pythagorean region of the spectrum. This greatly exaggerates the usefulness of Pythagorean tuning for harmony involving ratios of 7. Increasing this number beyond 14 would introduce new valleys into the charts, but with even less practical utility. However one should not forget that such a choice is available and so these are not the single-chain-of-fifths charts.

In 1/4-comma meantone we get a good approximation to a 4:7 ratio between Bb and G# (an augmented sixth), this is equivalent to stacking 10 fifths, Bb-F-C-G-D-A-E-B-F#-C#-G#. This is not as useful an approximation as the one we get in the super-Pythagorean (22-tET) region where only 2 stacked fourths (-2 fifths) are needed. If our scale were limited to 12 consecutive notes from the chain, then in the meantone region we'd have only two 4:7's while in the super-Pythagorean region we'd have ten of them. In the Pythagorean region we'd have none.

In the meantone region we get a good approximation to the just major third (a 4:5 frequency ratio) by stacking only 4 fifths, e.g. C-G-D-A-E. In the Pythagorean region 8 fourths is best. In 12-tET these two approximations are equivalent. In the super-Pythagorean region 9 fifths is best. In 17-tET 8 fourths is the same as 9 fifths. This is why I have used 12-tET and 17-tET as the boundaries of the Pythagorean region.

The first set of four charts shows only 5-limit intervals while the second set extends this to 7-limit. Limit here refers to the highest odd number that appears in any ratio.

The colours are intended to be mnemonic since primary colours are used for the odd numbers: 3-blue, 5-yellow, 7-red, and so ratios between odd numbers are the colour of the mixed paints; e.g. 3:5 (shown in superparticular form as 5:6) is green.

The error spectra for the different intervals are overlaid so it is clear at a glance where the good tunings lie, i.e. in the valleys. How low the valley goes is important, but it is also important that the valley not have steeply sloping sides. The slope of a line indicates how many fifths or fourths are needed to obtain the approximation to that interval. If it's steep it needs many, if it's shallow it needs few.

The dashed line is the RMS (root of mean of squares) combination of the errors in all the intervals on a given chart. This is an alternative to the maximum absolute value as given by the overlaying of the absolute error spectra.

Consistency is enforced in favour of the lone odd numbers (2:3, 4:5, 4:7) by the expedient of calculating the errors in the other intervals by subtracting the (signed) errors of the relevant pair of odd numbers. This may be less than optimum in some cases (but only near peaks).

If one's intention is purely to maximise 7-limit consonance in a single-chain-of-equal-fifths tuning, the main thing one learns from this is that there are really only three fifth-sizes (±1 cent) that are of interest, namely 697, 702 and 710 cents, although 714 cents (37-tET) and to a much lesser extent 694 cents, have some possibilities.

Here are the numbers of fifths required to approximate lone odd-number ratios up to 11, for each of these five fifth sizes. Those for ratios of two odd numbers can be found by subtraction. e.g. In the vicinity of 697 cents a 5:7 is best approximated by 10 - 4 = 6 fifths, and a 5:6 by 1 - 4 = -3 fifths. Remember, factors of 2 on either side of the colon ":" do not affect the result. Note that the 4:9 must be 2 fifths if consistency is to be maintained.

If you wish to see the errors in the individual intervals, or experiment with things like weighting the errors differently for different intervals, extending the results to 9-limit or 11-limit, or allowing more or fewer fifths to approximate the intervals, you are welcome to download the Excel 97 spreadsheet I used to generate the charts for both single and double chain tunings.
http://users.bigpond.net.au/d.keenan/Music/ChainOfFifthsTunings.xls.zip (94kB)
However I don't guarantee it will be easy to understand.